√ y=a(1+r)^t meaning 222082-Y=a(1+r)^t meaning

A quantity is decreasing exponentially if it decreases by the same percent in each time period C is the initial amount t is the time period (1 – r ) is the decay factor, r is the decay rate The percent of decrease is 100 r y = C (1 – r ) t W RITING E XPONENTIAL D ECAY M ODELS E XPONENTIAL D ECAY M ODEL 9In a labatory, a culture increases from 30 to 195 organisms in 5 hours What is the hourly growth rate in the growth formula y=a(1r)^t y=a(1r)^t The problem gives us y as 195 a as 30 t as 5 195=30(1r)^5 195/30 = (1r)^5 65 = (1r)^5 65^(1/5) = 1r 65^(2) = 1r 65^(2) 1 = r 1454 1 = r 0454 = r 454% = rQuestion Question 8 Of View Policies Current Attempt In Progress Find The Mean Of The Random Variable With The Probability Function Given 1 4 2 02 3 01 5 025 Px

I Don T Know If This Is Common Knowledge Here But The Smt 1 Intro Displays Snes Cpu Instructions For Some Reason Megaten

Y=a(1+r)^t meaning

Y=a(1+r)^t meaning-Y = A(1 – r)^t (the ^ is an important distinction, meaning "to the power of" t, whereas as you have the equation written right now, it says "divided" by t) So these are the variables we know A =3 T8RX → RX, T3(P) = AP Where A Is A Fixed Polynomial In RX' Exercise 2 Let TR2 Rbe The Linear Transformation Defined By T(x,y) = (a Y, Y Y) 1 Find Ker T And Ran T (kernel And Range) Of

What Is The Compound Interest Formula Robinhood

If we call P (t) the price of a financial asset (foreign exchange asset, stocks, forex pair, etc) at time t and P (t1) the price of the financial asset at t1, we define the daily return r (tP = C (1 r/n) nt where P = future value C = initial deposit r = interest rate (expressed as a fraction eg 006) n = # of times per year interest is compounded t = number of years invested Simplified Compound Interest Equation When interest is only compounded once per year (n=1), the equation simplifies to P = C (1 r) tSimply evaluate each component function at that value of tFor instance, if r → ⁢ (t) = t 2, t 2 t1 , then r → ⁢ (2) = 4, 1 We can sketch this vector, as is done in Figure 1211 (a) Plotting lots of vectors is cumbersome, though, so generally we do not sketch the whole vector but just the terminal

Exponential Growth = 3, Exponential Growth is 3, Explanation The formula is used where there is continuous growth in a particular variable such population growth, bacteria growth, if the quantity or can variable grows by a fixed percentage then the exponential formula can come in handy to be used in statisticsSection 18 Tangent, Normal and Binormal Vectors In this section we want to look at an application of derivatives for vector functions Actually, there are a couple of applications, but they all come back to needing the first oneP = C (1 r/n) nt where P = future value C = initial deposit r = interest rate (expressed as a fraction eg 006) n = # of times per year interest is compounded t = number of years invested Simplified Compound Interest Equation When interest is only compounded once per year (n=1), the equation simplifies to P = C (1 r) t

A Concise Reduction Obliquely Naming Your Meaning ) ACRONYM A Clever ReOrganisation Nudges Your Memory ) ACRONYM Alphabetical Character Rendition Of a Name Yielding a Meaning ) ACRONYM Academy's Choice Reading, One Newspaper for You and Me (Newspaper of IMSA) ACRONYM A Cross Reference Of Notes Yielding Messages ) ACRONYMX=−2 cost, y= 2,z= 3 −sint Therefore, the curve is contained in the planey= 2, and the following holds (x2)2(z−3)2= cos2tsin2t= 1 We conclude that the curver(t)is the circle of radius 1 in the planey= 2 centered at the point(−2,2,3) 250 May 16, 11 SECTION131VectorValued Functions(LT SECTION 141)251 5This means it is a function that changes at a constant percent rate So, A is your function (or the "answer") P is the initial value (or your "starting point") (1r) is the base (or in this case your "growth factor" if this value is greater than 1 or "decay factor" if it is less than zero) t is the time (or the time for or since growth)

Exponential Growth Decay Word Problems Video Khan Academy

Mathematics Libraries

Exponential Growth = 100 * (1 10%) ^36;R Operators An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations R language is rich in builtin operators and providesT = Thymidylic acid U = Uridylic acid I = Inosylic acid should be obvious codes F = Phe = Phenylanine N = Asn = Asparagine R = Arg = Arginine Y = Tyr = Tyrosine are phonetic codes R = A or G = puRine Y = C or T = pYrimidine K = G or T = Keto M = A or C = aMino S = G or C = Strong base pair W = A or T = Weak base pair double base codes D

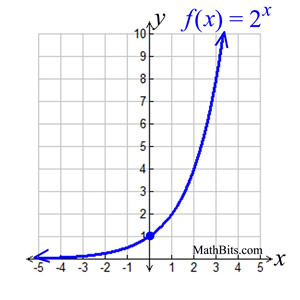
Exponential Functions Mathbitsnotebook A1 Ccss Math

Simple Regression Assignment

A distribution T is 0 if and only if its support is empty If ∈ ∞ is identically 1 on some open set containing the support of a distribution T then fT = T If the support of a distribution T is compact then it has finite order and furthermore, there is a constant C and a nonnegative integer N such thatX(t) = x 0 × (1 r) t x(t) is the value at time t x 0 is the initial value at time t=0 r is the growth rate when r>0 or decay rate when rIn mathematics and its applications, the root mean square (RMS or rms) is defined as the square root of the mean square (the arithmetic mean of the squares of a set of numbers) The RMS is also known as the quadratic mean and is a particular case of the generalized mean with exponent 2 RMS can also be defined for a continuously varying function in terms of an integral of the squares of the

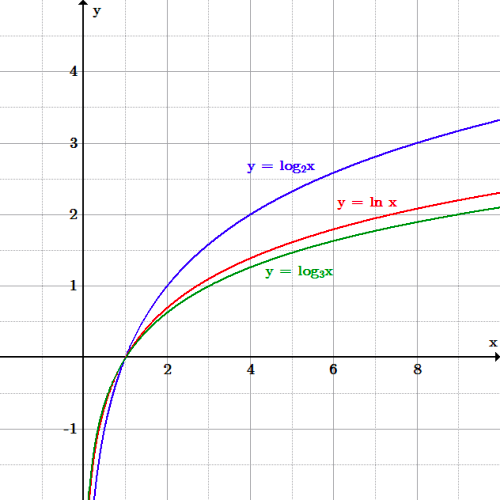
The Real Number E Boundless Algebra

When Is Y A Vowel Or Consonant Merriam Webster

~y= A~x , 2 4 y 1 y 2 y 3 3 5= 2 4 a 11 a 12 a 21 a 22 a 31 a 32 3 5 x 1 x 2 = 2 4 a 11x 1 a 12x 2 a 21x 1 a 22x 2 a 31x 1 a 32x 2 3 5 =x 1 2 4 a 11 a 21 a 31 3 5x 2 4 a 12 a 22 a 32 3 5 (C) = 2 4 (a 11;a 12) ~x (a 21;a 22) ~x (a 31;a 32) ~x 3 5 (R) There are two2 fundamentally different yet equivalent ways to interpret the matrixLet, y = a^x Taking logarithm on bothsideboth side ln(y)=x * ln(a) Differentiating both side wrt x d/dx{ln(y)} =d/dx{x*ln(a)} (1/y)dy/dx = x*0 ln(a)*1=ln(a) dy/dx = y*ln(a) = a^x * ln(a) Sign In Derivatives and Differentiation (mathematics)O f t h e A r m y , A n a l y s i s a n d I n t e g r a t i o n C e l l ( A A A I – C L ) , 1 0 5 A r m y P e n t a g o n , Washington, DC 310–0105 Further, if i t i s d e t e r m i n e d t h a t a n e s t a b l i s h e d "group" identified within this regulation, later takes on the characteristics of a com

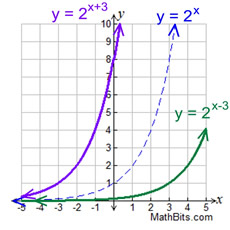
Exponential Functions Mathbitsnotebook A1 Ccss Math

Inverse Function Wikipedia

Y ~ (A B C)^2 y ~ A*B*C ABC Three factor experiment but with a model containing main effects and two factor interactions only Both formulae specify the same model y ~ A * x y ~ A/x y ~ A/(1 x) 1 Separate simple linear regression models of y on x within the levels of A, with different codingsGiven, 1111=R If we add the numbers present in the given number then, =>1111=4(FOUR) Last letter is R So again for 2222=T =>2222=8(EIGHT) Last letter is T 3333=E =>3333=12(TWELVE) Last letter is E 4444=N =>4444=16(SIXTEEN) LastAn operator is a symbol that operates on a value or a variable For example is an operator to perform addition In this tutorial, you will learn about different C operators such as arithmetic, increment, assignment, relational, logical, etc with the help of examples

2

Dea1 Matallkomplexe Google Patents

O f t h e A r m y , A n a l y s i s a n d I n t e g r a t i o n C e l l ( A A A I – C L ) , 1 0 5 A r m y P e n t a g o n , Washington, DC 310–0105 Further, if i t i s d e t e r m i n e d t h a t a n e s t a b l i s h e d "group" identified within this regulation, later takes on the characteristics of a comGoogle's free service instantly translates words, phrases, and web pages between English and over 100 other languagesI was reading the documentation on R Formula, and trying to figure out how to work with depmix (from the depmixS4 package) Now, in the documentation of depmixS4, sample formula tends to be something like y ~ 1For simple case like y ~ x, it is defining a relationship between input x and output y, so I get that it is similar to y = a * x b, where a is the slope, and b is the intercept

What Is The Compound Interest Formula Robinhood

I Don T Know If This Is Common Knowledge Here But The Smt 1 Intro Displays Snes Cpu Instructions For Some Reason Megaten

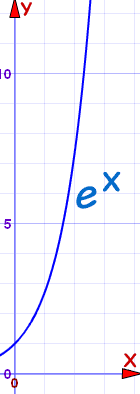
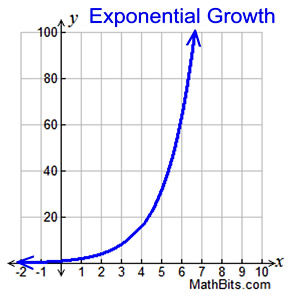
Services APTC Army Physical Training Corps GB AR Assam Rifles I ARCS Australian Red Cross Society AUS ARUAIF Australian Remount Unit AUS ASC ArmyAlthough it may b e somewhat u n r e a l i s t i c i n p r a c t i c e , i t e n a b l e s comparisons t o b e made between The r e a d e r can, o f c o u r s e , u s e an a l t e r n a t i v e d e f i n i t i o n t o s u i t h i s p u r p o s e f o r most o f t h e methods recommended 18 27 a cV cS NOTATION n C (xi x j 3 (n1) (n2) (Eq 2A function of the form y=a(1 r)t, where a> 0 and r> 0, is an exponential growth function initial amount time growth factor rate of growth (in decimal form) final amounty=a(1 r)t WWhat You Will Learnhat You Will Learn Use and identify exponential growth and decay functions Interpret and rewrite exponential growth and decay functions

Solved Please Show All The Work To Complete The Question Chegg Com

Exponential Growth And Decay

I was reading the documentation on R Formula, and trying to figure out how to work with depmix (from the depmixS4 package) Now, in the documentation of depmixS4, sample formula tends to be something like y ~ 1For simple case like y ~ x, it is defining a relationship between input x and output y, so I get that it is similar to y = a * x b, where a is the slope, and b is the interceptX a (nonempty) numeric vector of data values y an optional (nonempty) numeric vector of data values alternative a character string specifying the alternative hypothesis, must be one of "twosided" (default), "greater" or "less"You can specify just the initial letter106 Exponential Growth and Decay Exponential decay equation #1 – y = a (1 – r) t y = what's leftover a = what you start with r = rate t = time ex Timmy drank hot chocolate which has 110 milligrams of sugar If the sugar was eliminated from the body at a rate of 12% per hour How long will it take for half of the sugar to be gone from his body?

2

11 2 Half Life Chemistry Libretexts

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreSolve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponent# A formula y ~ x # A converted formula y = a_1 a_2 * x This is an example of a simple conversion y ~ x gets translated into y = a_1 a_2 * x To see and understand what R actually happens, you can use the model_matrix() function This function creates a design or model matrix by, for example, expanding factors to a set of dummy variables, depending on the contrasts, and expanding interactions similarly

Solved The Following 14 Data Pairs Relate Variable X 1 T Chegg Com

Exponential Functions Mathbitsnotebook A1 Ccss Math

For example if the variable were named rgbImage, then we'd know what "A" represented As of now, we don't You didn't supply any context either so we're left to speculate (or just ignore the question which is probably what most people did)Where b is a positive real number, and the argument x occurs as an exponent For real numbers c and d, a function of the form () = is also an exponential function, since it can be rewritten as = () As functions of a real variable, exponential functions are uniquely characterized by the fact that the growth rate of such a function (that is, its derivative) is directly proportional to theSection 18 Tangent, Normal and Binormal Vectors In this section we want to look at an application of derivatives for vector functions Actually, there are a couple of applications, but they all come back to needing the first one

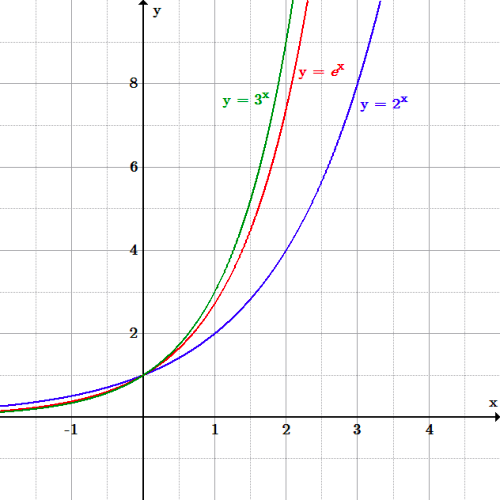
E Mathematical Constant Wikipedia

U02c6 R Xy A Interpret The Meaning Of The Y Intercept And The Slope Of The Course Hero

If we call P (t) the price of a financial asset (foreign exchange asset, stocks, forex pair, etc) at time t and P (t1) the price of the financial asset at t1, we define the daily return r (tThe general equation for depreciation is given by y = A(1 – r)t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years A car was purchased 6 years ago for $25,000 If the annual depreciation rate is 11%, which equation can be used to determine the approximate current value of the car?( 4) F or t he pur pos e of pa r a gr a ph ( 1) (c) , a pe r s on hol ds a uni t i n a bus i ne s s t r us t i f h e h a s a l e ga l or a n e qui t a bl e i nt e r e s t i n t ha t uni t Meaning of control of voting in Part IVA of Act 4

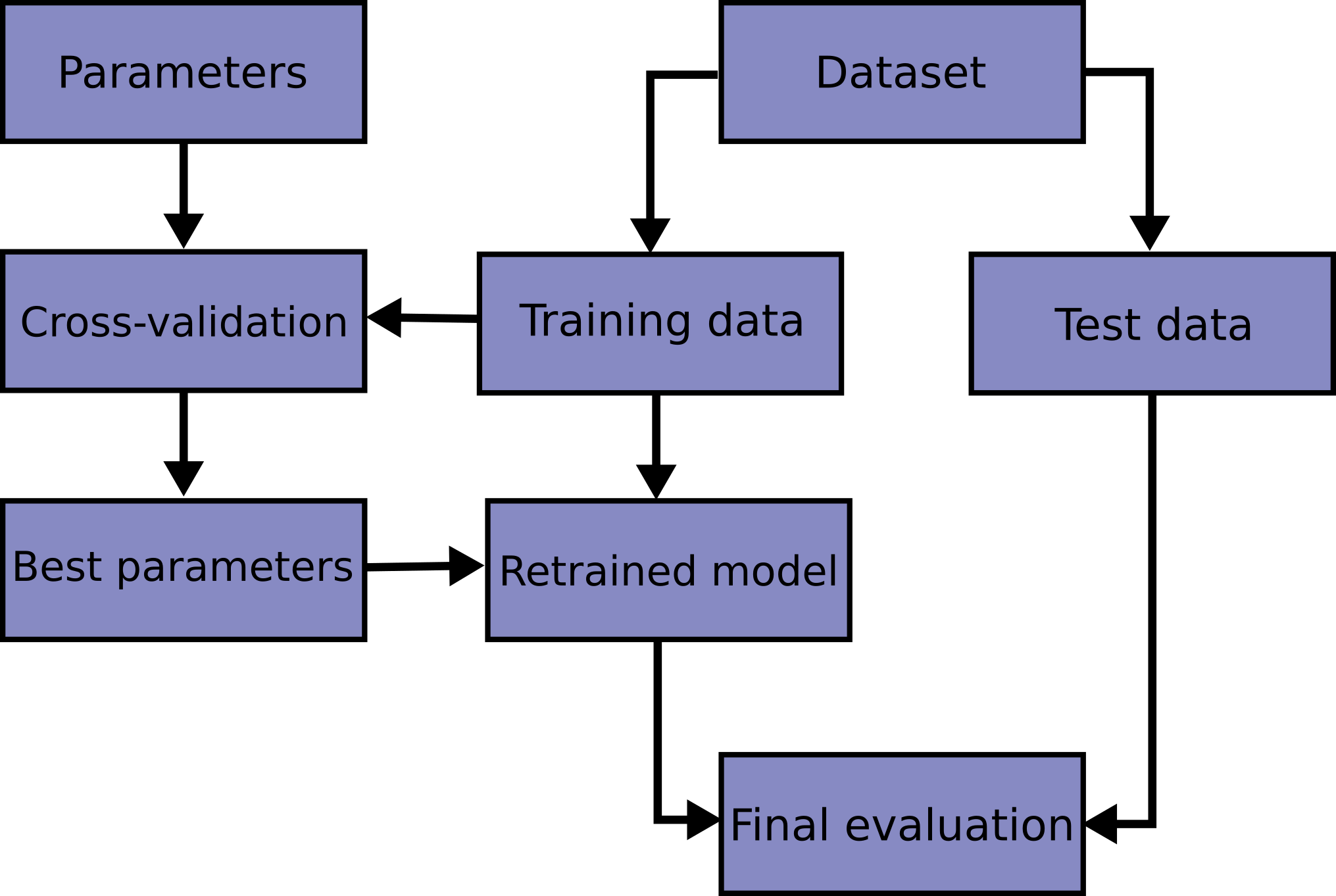
3 1 Cross Validation Evaluating Estimator Performance Scikit Learn 0 24 1 Documentation

The Regression Equation Introduction To Statistics

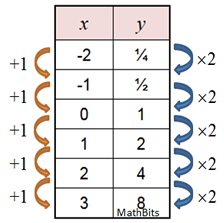
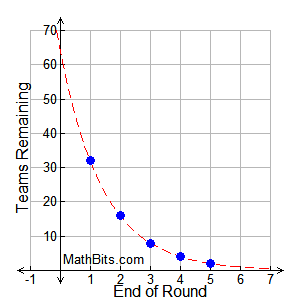
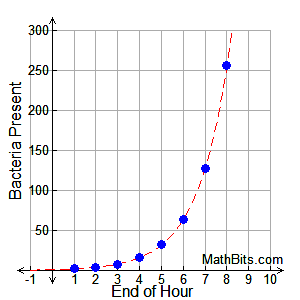
Using the growth formula we have y = a(1 r) x where a = 1 (we start with 1 bacteria), and r = 100%, since the amount doubles y = 1(1 100) x = 2 x (same result) Notice that the graph is a scatter plot You cannot have a fractional part of a bacteria The dotted line is the exponential function which contains the scatter plots (the model)1 Answer1 Active Oldest Votes 4 A better formula to use would be y = a ( 1 r k) k t, where k is the number of times the interest is compounded per year So, plugging in your information gives y = 3750 ( 1 06 12) 132 = $ ShareO f t h e A r m y , A n a l y s i s a n d I n t e g r a t i o n C e l l ( A A A I – C L ) , 1 0 5 A r m y P e n t a g o n , Washington, DC 310–0105 Further, if i t i s d e t e r m i n e d t h a t a n e s t a b l i s h e d "group" identified within this regulation, later takes on the characteristics of a com

Formula For Continuously Compounding Interest Video Khan Academy

Ars 1 Fars Htm Ars 18

The next function we look at is qnorm which is the inverse of pnorm The idea behind qnorm is that you give it a probability, and it returns the number whose cumulative distribution matches the probability For example, if you have a normally distributed random variable with mean zero and standard deviation one, then if you give the function a probability it returns the associated Zscore1 1 Introduction R is a system for statistical computation and graphics It provides, among other things, a programming language, high level graphics, interfaces to other languages and debugging facilities This manual details and defines the R languageAccording to the statutes of the United Orders of the Temple and Saint John of Jerusalem, etc, the standard of Saint John is described as gules, on a Cross Argent, the Agnus Deimeaning Red on a Silver Cross with a representation of the Lamb of Godwith the letters FERT

Partc Chapter5 4 5

What Is The Compound Interest Formula Robinhood

Evaluating a vectorvalued function at a specific value of t is straightforward;2 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all xA period of one time constant (t=¿ = 1) the output has decayed to y(¿) = e¡1y(0) or 368% of its initial value, after two time constants the response is y (2 ¿ ) = 0 135 y (0) Several flrstorder mechanical and electrical systems and their time constants are shown in Fig

2

Exponential Functions Compound Interest

According to the statutes of the United Orders of the Temple and Saint John of Jerusalem, etc, the standard of Saint John is described as gules, on a Cross Argent, the Agnus Deimeaning Red on a Silver Cross with a representation of the Lamb of Godwith the letters FERTT) RX R2 T(P) = (PO) P'(0));

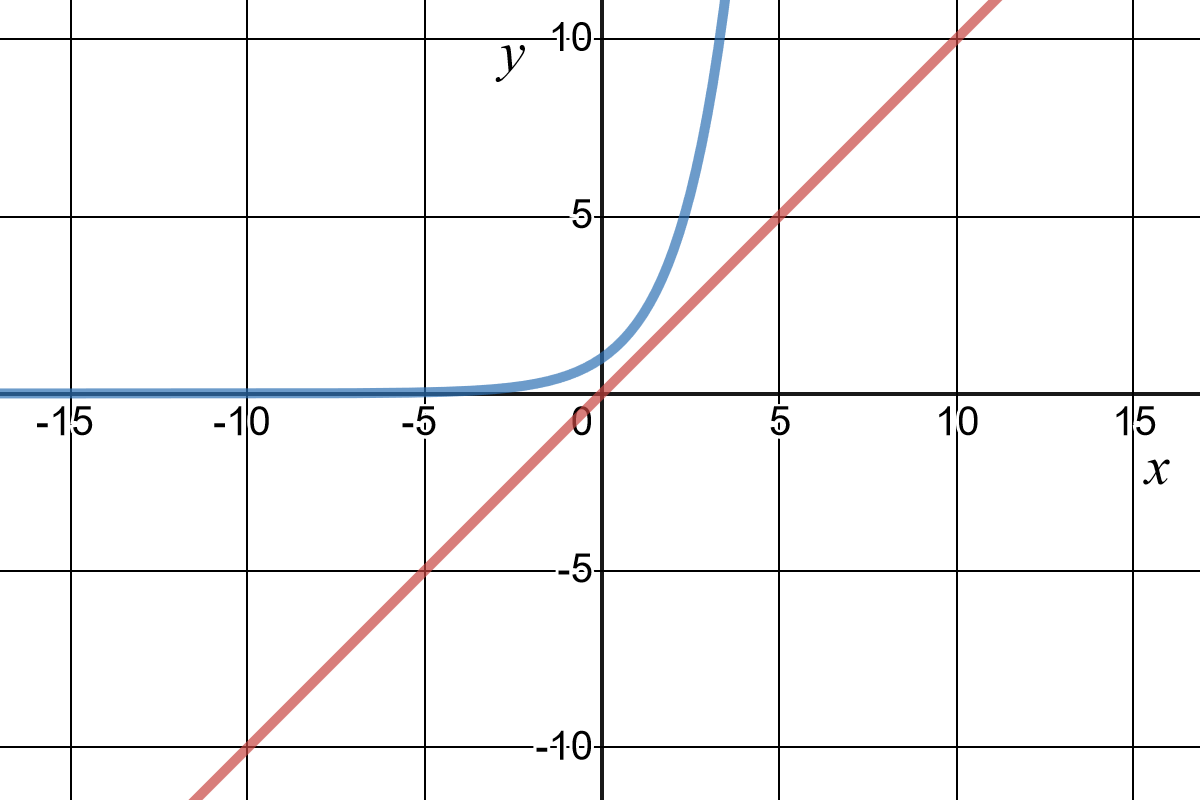
Linear Vs Exponential Functions Expii

Linear Regression Simple Steps Video Find Equation Coefficient Slope Statistics How To

Pdf Prolog En 10 Figures

Solved 30 Short Answer Questions Worth 2 Marks Each For A Total Of 60 Marks 1 Given S P 1 Rt Solve For T 2 What Is The Meaning Of The Y Interc Course Hero

1 Normal Modes Of Mechanical Vibrations Of A Circ Chegg Com

Minimum Values Definition Concept Video Lesson Transcript Study Com

Graphing Parabolas

A Familial Cluster Of Pneumonia Associated With The 19 Novel Coronavirus Indicating Person To Person Transmission A Study Of A Family Cluster The Lancet

Economics Mit Edu Files 7181

Plotting Multiple Variables

Linear Relationship Definition

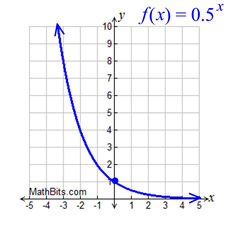
Exponential Functions Mathbitsnotebook A1 Ccss Math

Dea1 Matallkomplexe Google Patents

3

What Do Correlation Coefficients Positive Negative And Zero Mean

Eprints Illc Uva Nl Id Document

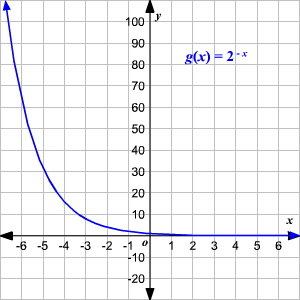
Domain And Range Of Exponential And Logarithmic Functions

9 1 Exponential Functions Exponential Functions A Function Of The Form Y Ab X Where A 0 B 0 And B 1 Characteristics 1 Continuous And One To One Ppt Download

The Formula For The Cross Product Math Insight

2

1

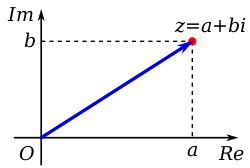
Complex Number Wikipedia

Possible Vector Solution For Synthetic Geometry Involving Parallelogram And Triangle Sharing Centroid Mathematics Stack Exchange

Introduction To Exponential Functions

Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 718 10 14 abs value notes Pdf

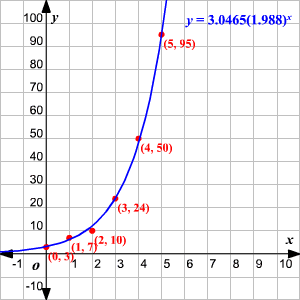
Exponential Regression

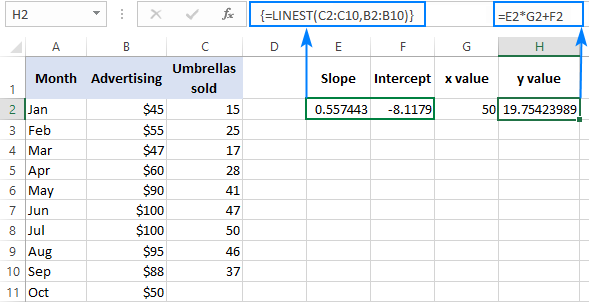
Excel Linest Function With Formula Examples

Exponential Functions Mathbitsnotebook A1 Ccss Math

The Real Number E Boundless Algebra

Exponential Growth Relationship Where The Initial Starting Amount Increases By The Same Percent Over A Given Period Of Time Ppt Download

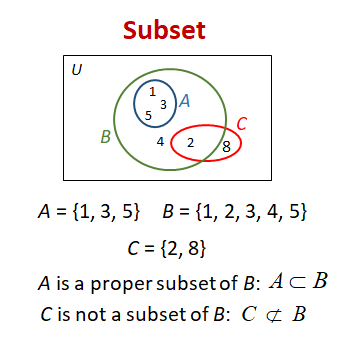
Subsets Video Lessons Examples And Solutions

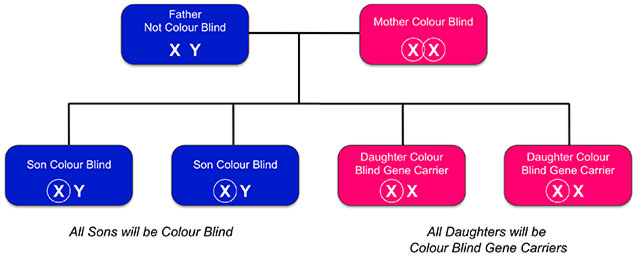
Inherited Colour Vision Deficiency

Exponential Functions Mathbitsnotebook A1 Ccss Math

R Programming Language Wikipedia

Projecteuclid Org Download Pdf 1 Euclid Mjms

What Do Correlation Coefficients Positive Negative And Zero Mean

R Programming Language Wikipedia

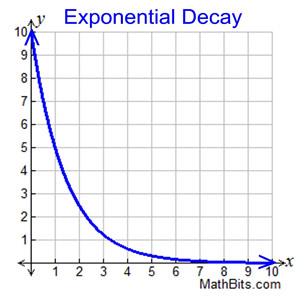
Exponential Decay Definition And Function

Tndsrilanka

6 10 Total Points A 6 Points Recall That Th Chegg Com

2

Exponential Functions Mathbitsnotebook A1 Ccss Math

Solved 2 Assume A Closed Smooth Curve Y A B R2 Chegg Com

Search Q Compound Formula Chemistry Tbm Isch

Exponential Functions Mathbitsnotebook A1 Ccss Math

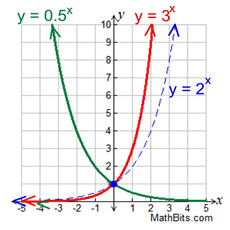
Exponential Functions Mathbitsnotebook A1 Ccss Math

Morphological Analysis And Diacritical Arabic Text Compression Semantic Scholar

Exponential Decay Definition And Function

Www3 Nd Edu Wevans1 Ecoe Ps2 Pdf

Function Definition Types Examples Facts Britannica

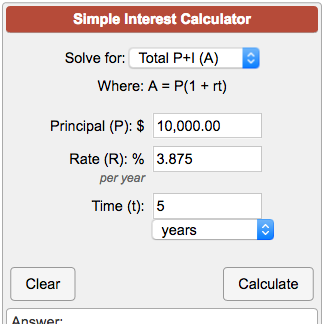
Simple Interest Calculator A P 1 Rt

Wn Courtney Kessler

Power System Analysis Material Mathankumar S Vmkvec

Regression Basics For Business Analysis

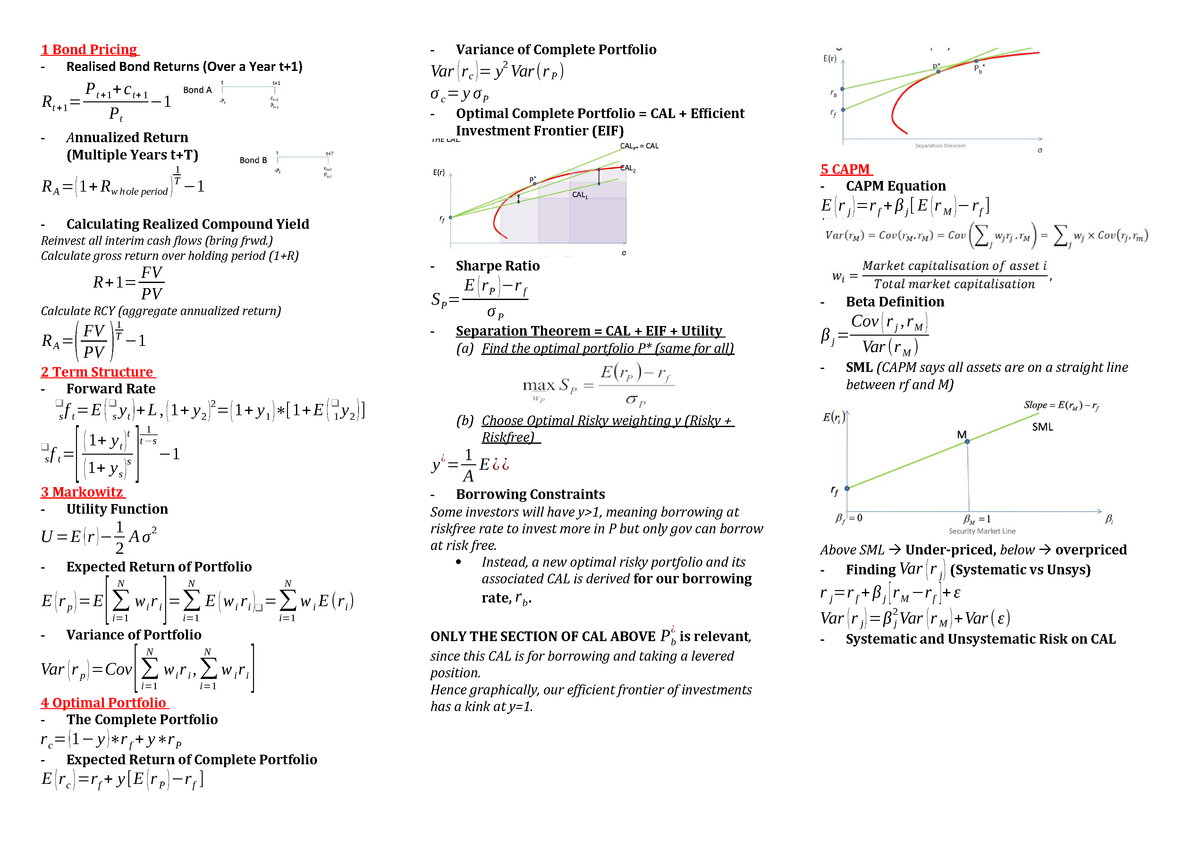
2624 Final Formula Sheet Fins2624 Studocu

Exponential And Logarithmic Functions Logarithmic Functions Sparknotes

13 For A Particle Of Mass M Moving In Two Dimensi Chegg Com

Ieeexplore Ieee Org Iel7 153 Pdf

Applying The Continuous Exponential Growth Model Pert Youtube

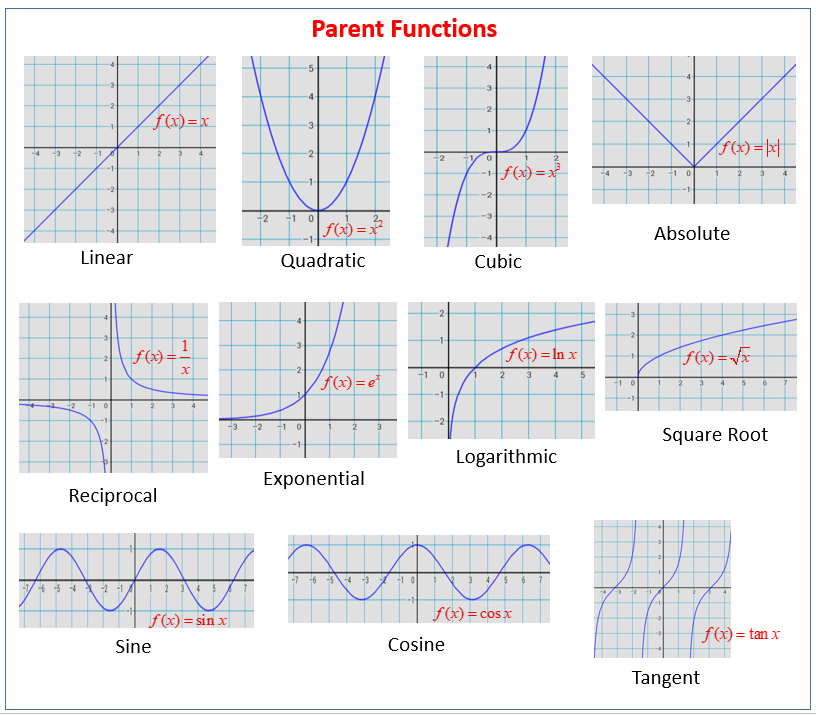
Parent Functions And Their Graphs Video Lessons Examples And Solutions

Graphing Parabolas

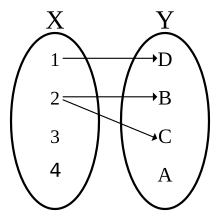
Function Mathematics Wikipedia

R Squared Definition Interpretation And How To Calculate

Q Tbn And9gcqijosvjs X3b0gges Uh2g7tqf4q8ek Jt2uxlutl7txidqktm Usqp Cau

Counting Processes

Nanginginig In English Meaning

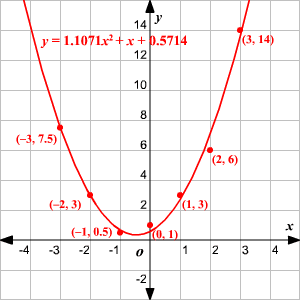
Quadratic Regression

Graphing Parabolas

Minimum Values Definition Concept Video Lesson Transcript Study Com

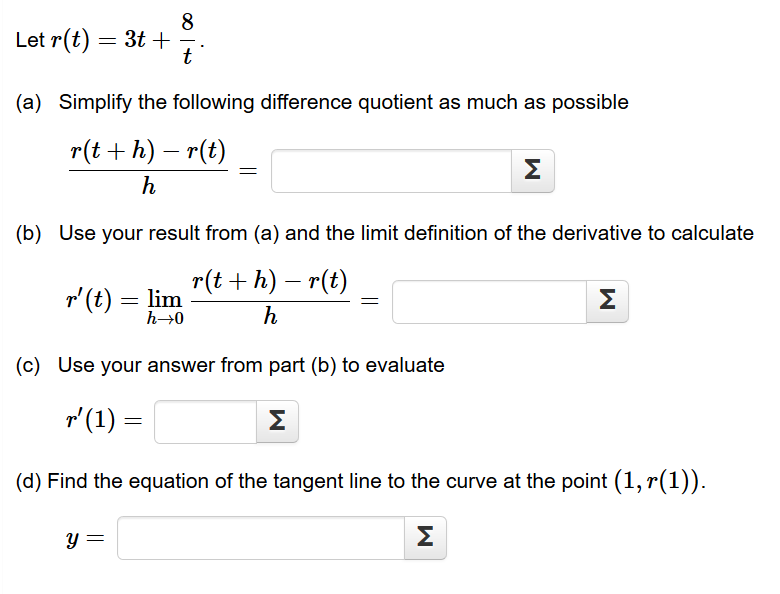
Solved Let R T 3 A Simplify The Following Differe Chegg Com

If X And Y Are Connected Parametrically By The Equations Given W

What Is The Compound Interest Formula Robinhood

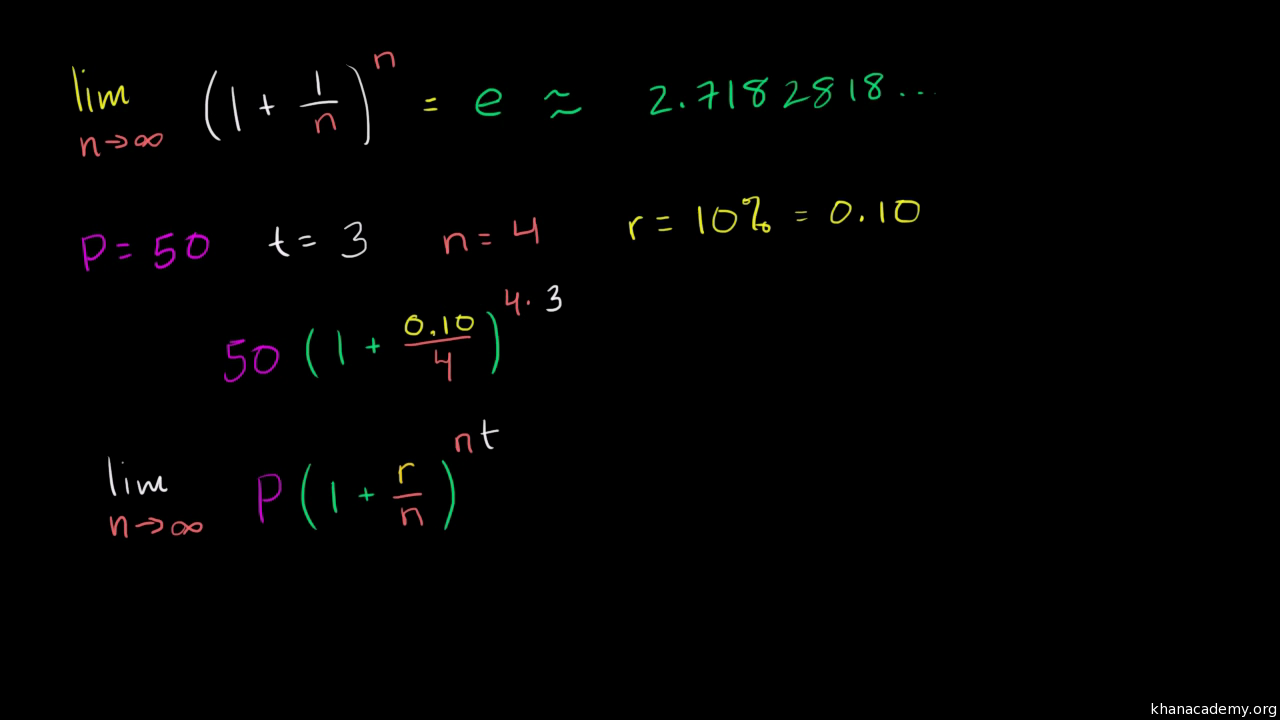
Formula For Continuously Compounding Interest Video Khan Academy

Exponential Decay Definition And Function

Why Are A E I O U And Y Called Vowels Dictionary Com

Introduction To Exponential Functions

Incoming Term: y=a(1+r)^t meaning, what is y=a(1+r)^t, y=a(1+r)^t solve for r,